미분 (derivative)
1) 함수에 대한 입력의 순간변화량에 대한 출력의 순간변화량의 비율을 도출
2) 임의의 점에 접하는 직선의 기울기
- e.g. 시간에 따른 이동거리를 나타내는 함수가 있을 때, 특정 시각에 속도를 구하고자 한다. 하지만, 움직이는 자동차의 사진을 찍었을 때, 속도나 속력을 알 수 없듯이 해당 시각의 정확한 속도를 구하는 것에는 모순이 있다. 그래서 매우 짧은 시간과 이동 거리에 따른 속력을 구한다. 아래의 사진은 유튜브 3Blue1Brown에서 가져왔음.
- 해당 부분에서 시각은 얼마든지 변해도 상관이 없기 때문에 이를 함수로 나타낼 수 있다.

도함수 (derivative)
1) 함수가 주어질 때, 각각의 x의 값에 미분계수가 하나씩 대응되는 함수
$$\mathop {\lim }\limits_{\Delta \to 0} \frac{{f\left( {x + \Delta } \right) - f\left( x \right)}}{\Delta }$$
- 0으로 수렴한다는 것은 완전히 0이거나 작은 값이 아님.
미분 (differentiation)
1) 미분 (=도함수)를 구하는 과정을 지칭
상미분 (ordinary derivative)
1) 변수가 하나인 함수의 미분
$$\frac{d}{dx}\{f(x) + g(x)\} = \frac{df(x)}{dx} + \frac{dg(x)}{dx}$$
멱함수 (power function)
1) 변수를 특정 상수로 거듭제곱하는 함수
$$f(x) = cx^\alpha$$
합성함수 (composite function)
1) 함수의 공역을 다른 함수의 정의역으로 유도된 함수 (함수의 출력을 다른 함수의 입력으로 넣는 것)
$$g(f(x)) = (g \circ f)(x)$$
연쇄법칙 (chain rule)
1) 합성함수를 미분하는 방법으로 1개 이상 합성된 함수에 대해서 연쇄적으로 미분하는 공식
$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dv} \cdot \frac{dv}{dw} ... \frac{d?}{dx}$$
2) 다항함수 chain rule 공식
$$\frac{dh}{dt} = \nabla f(g(t)) \cdot g'(t)$$
곱의 법칙 (product rule)
1) 함수가 2개 이상의 함수의 곱으로 표현될 수 있을 경우 각각을 미분하는 법칙
$$h'(x) = (yz)' = y'z + yz'$$
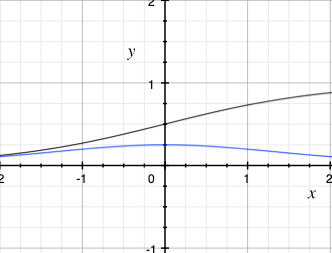
시그모이드 함수 (sigmoid function)
$$\varsigma_{a}(x) = \frac{1}{1 + e^{-ax}}$$
1) 로지스틱 회귀분석에서 데이터를 0, 1 두가지로 분류할 때, 활성화 함수인 시그모이드 함수를 사용
2) 단점
- Gradient vanishing 현상 (sigmoid function의 미분값에서 input x의 절대값이 커질 수록 0으로 수렴하여
backpropagation시 미분값이 사라질 수 있음
- 함수값 중심이 0이 아니기 때문에 학습 속도가 느려짐
ReLU 함수 (rectified linear unit)
$$\phi (x) = max(0, x)$$
1) x가 0보다 클 경우에만 성립
2) 0을 기점으로 기울기가 급변하는 특징

참고 교재 : www.yes24.com/Product/Goods/66913718 (인공지능을 위한 수학)
'Math > Calculus' 카테고리의 다른 글
| 자코비안 (Jacobian) (0) | 2021.02.03 |
|---|---|
| 라플라시안 (Laplacian) (0) | 2021.02.03 |
| 발산 (Divergence) & 회전 (Curl) (0) | 2021.02.02 |
| 벡터 함수의 미분 (0) | 2021.01.31 |
| 편미분 (partial derivative) (0) | 2021.01.28 |
