벡터 함수
1) 정의
- 벡터 함수의 미분은 각각의 요소를 미분하는 것과 같다.
- 최초의 함수를 시간 함수로써 위치를 제공하는 것으로 해석한다면, 미분은 속도(velocity)벡터를 제공한다.
$$\frac{d}{dt} \begin{bmatrix} {x(t)} \\{y(t)} \end{bmatrix}=\begin{bmatrix} {x'(t)} \\ {y'(t)} \end{bmatrix}$$
2) 설명
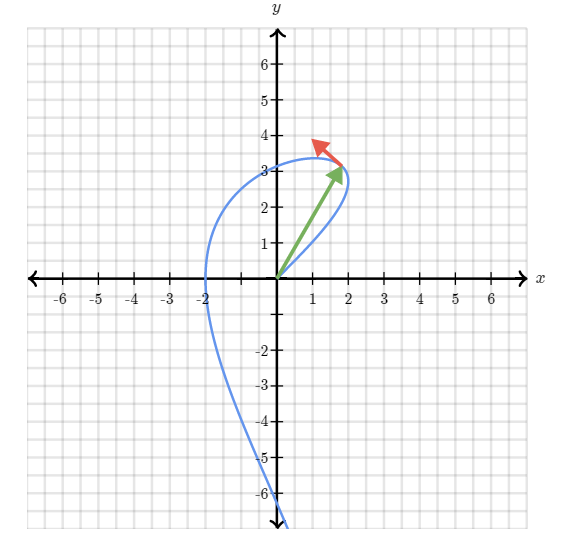
- 파란색 선은 초기 함수의 벡터 값의 끝점을 이은 선이고 초록색 선을 특정 n값에서의 벡터를 나타낸 것이다.
- 위의 식에서 미분을 이후에 나타난 두 함수 값은 여전히 2차원 상의 벡터 값으로 표현할 수 있는데 같은 n값을 넣은 경우이다. 이때, 초기 함수의 속도 벡터를 의미한다.
곡률 (Curvature)
1) 정의
- 단위 탄젠트 벡터는 곡선의 방향과 얼마나 빠른 속도로 회전을 하는 비율을 나타낸다.
- 곡률반지름의 역수 (반지름이 커질수록 곡률은 줄어든다.)
$$\kappa = \dfrac{1}{R}$$
2) 계산
(1) 특정 지점에서의 단위 탄젠트 벡터를 찾는다.
- 위에서 나온 벡터 함수의 미분을 사용하여 특정 n에서의 속도 벡터를 구한다.
- 속도 벡터의 값을 단위 벡터로 표현하기 위해서 해당 벡터의 스칼라 값을 나누어 준다.
$$T(t) = \frac {\vec{s'}(t)} {||\vec{s'}(t)||}$$
(2) 곡선을 어느정도의 속도로 이동하느냐에 달려있기 때문에 특정 n에서 미분하는 것이 아니라 arc length에서 미분을 한다.
$$\kappa = ||\frac {dT} {ds}||$$
- 그럼에도 불구하고, 일반적으로 t와 관련하여 T의 미분을 하고 s벡터의 미분 값으로 나눈다.
$$\kappa = ||\frac {dT} {ds}|| = \frac {|| \frac {dT}{dt}||} {||\frac {d\vec{s}}{dt}||}$$
'Math > Calculus' 카테고리의 다른 글
| 자코비안 (Jacobian) (0) | 2021.02.03 |
|---|---|
| 라플라시안 (Laplacian) (0) | 2021.02.03 |
| 발산 (Divergence) & 회전 (Curl) (0) | 2021.02.02 |
| 편미분 (partial derivative) (0) | 2021.01.28 |
| 미분 기본 (0) | 2020.12.30 |
