Support Vector Machine
- 고차원 데이터 분류에 좋은 성능을 보인다.
- 퍼셉트론의 확장
- 최적화 대상은 margin을 최대화하는 것
margin : 클래스를 구분하는 결정 경계와 결정 경계와 가장 가까운 sample사이의 거리로 정의
이때 해당 sample을 support vector라고 부름
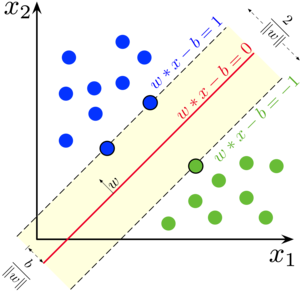
선형 SVM
1) 개요
- 클래스가 다른 데이터들을 large margin으로 분리하는 경계를 찾는 것이다.
- 즉, 클래스 간의 거리가 최대가 될 수 있도록 하는 것이다.
2) 수학적 이해 - w, b를 찾아야한다.
- 목적식
$$w^{T}x_{pos} + b = 1 \;\;vector\;on\;plus\;plane$$
$$w^{T}(x_{neg}+\lambda w) + b = 1 \;\; (x_{pos} = x_{neg}+\lambda w)$$
$$w^{T}x_{neg} + b + \lambda w^{T}w=1$$
$$-1 + \lambda w^{T}w=1 \;\; (w^{T}x_{neg}+b = -1)$$
$$\lambda = \frac{2}{w^{T}w}$$
$$Margin = distance(x_{pos}, x_{neg})$$
$$=||x_{pos}-x_{neg}||_{2}$$
$$=||(x_{neg}+\lambda w) - x_{neg}||_{2}$$
$$=||\lambda w||_{2}=\lambda \sqrt{w^{T}w}$$
$$=\frac{2}{w^{T}w}\cdot \sqrt{w^{T}w}= \frac{2}{\sqrt{w^{T}w}}$$
$$=\frac{2}{||w||_{2}}$$
L2 norm
$$||W||_{2}=(\sum_{i} |w_{i}|^{2})^{\frac{1}{2}} = \sqrt{w_{1}^{2}+w_{2}^{2} + \cdots +w_{n}^{2}} = \sqrt{W^{T}W}$$
$$max\;Margin = max\frac{2}{||w||_{2}} \Leftrightarrow min\frac{1}{2}||w||_{2}$$
- 계산의 편의를 위해 제곱을 해준다.
$$\boldsymbol{\frac{1}{2}||w||_{2}^{2}}$$
- 제약식
- 아래 제약을 통해 margin이 최소 1 이상인 값을 구한다.
$$w_{0}+w^{T}x^{(i)}\geq 1\;\;y^{(i)}=1\;일\;때$$
$$w_{0}+w^{T}x^{(i)}\leq -1\;\;y^{(i)}=-1\;일\;때$$
$$\boldsymbol{y_{i}(w_{0}+w^{T}x_{i})\geq 1}\;\; \forall i$$
Quadratic programming
- 목적함수는 제곱을 했기 때문에 2차식이고 제약식은 선형이기 때문에 이를 quadratic programming이라 부른다.
- 이는 convex optimization이기 때문에 globally optimal solution이 존재한다.
다음 공식을 적용하여 L2 norm을 사용한 것을 알 수 있다.
$$Ax+By+c=0,\;(x_{0}, y_{0})\;\;d=\frac{Ax_{0}+By_{0}+c=0}{\sqrt{A^{2}+B^{2}}}$$
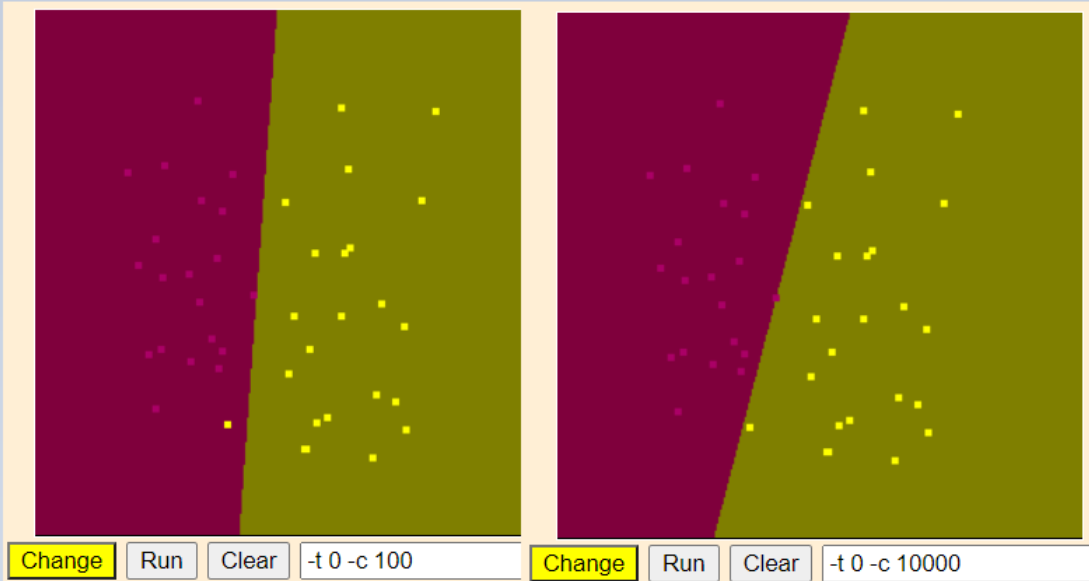
선형 SVM 이상치 처리 (linearly non-separable data)
1) Outlier (이상치 처리)
- 실전에서 모델을 설계할 때, 모든 데이터가 정확하게 나뉘어 있는 경우는 드물다.
- 선형 SVM에서는 parameter cost를 조정하여 얼마나 다른 클래스로 분류될 허용치를 결정한다.
- C의 크기가 작을 수록 많이 허용하고 클수록 적게 허용한다.
- C가 없으면 hard-margin SVM (separable), 있으면 soft-margin SVM (non-separable)으로 나뉜다.
2) Slack variable
- 선형 제약 조건을 완화
- 제약식
$$w_{0}+w^{T}x^{(i)}\geq 1-\xi\;\;y^{(i)}=1\;일\;때$$
$$w_{0}+w^{T}x^{(i)}\leq -1+\xi\;\;y^{(i)}=-1\;일\;때$$
- 목적식
$$\frac{1}{2}||w||^{2}+C(\sum_{i}\xi^{(i)})$$
3) 코드 예시
from sklearn.svm import SVC
svm = SVC(kernel='linear', C=10.0, random_state = 1)
svm.fit(X_train_std, y_train)
비선형 SVM
1) 개요
- 비선형 데이터를 매핑 함수(phi function)를 사용하여 선형적으로 구분되는 고차원 공간에 투영한다.
- SVM을 고차원의 투영된 공간에서 학습을 진행한다.

2) 수학적 이해
$$\Phi : x \rightarrow z = \Phi(x)$$
- SVM Lagrangian dual formulation에서 x를 내적하는 부분이 있는데 이를 아래와 같이 변환한다.
$$x_{i}^{T}x_{j} \rightarrow \Phi(x_{i})^{T}\Phi(x_{j})$$
- 내적에 사용되는 높은 비용 절감을 위해 커널함수로 정의
$$K(x^{(i)},x^{(j)})=\phi(x^{(i)})^{T}\phi(x^{(j)})$$
kernel function을 사용하면 phi function을 사용했을 때와 동일한 결과지만 계산과정은 더 간단하다.
3) Kernel function
- kernel을 결정하는 뚜렷한 기준이 없어서 데이터 특성에 맞게 선택하는 것이 중요하다.
4) RBF; Radial Basis function (방사기저함수, Gaussian kernel)
- 가장 널리 사용되는 커널 함수 중 하나
- 매개변수 C와 gamma를 조정해야 하는데 gamma는 가우시안 구의 크기를 제한하는 매개변수이다.
- gamma가 클수록 support vector의 영향력이 줄어들어 결정경계는 구불구불해진다.

5) 코드 예시
svm = SVC(kernel='rbf', random_state = 1, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)Logistic vs. SVM
- Logistic은 SVM보다 이상치에 민감하다. SVM은 결정 경계에 가까운 support vector에 관심을 둔다.
- Logistic은 간단하고 구현이 쉬우며 업데이트가 용이하다.
from sklearn.linear_model import SGDClassifier
ppn = SGDClassifier(loss = 'perceptron') # perceptron
lr = SGDClassifier(loss = 'log') # logistic regression
svm = SGDClassifier(loss = 'hinge') # SVM
참고
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 (길벗)
비스카이비전 블로그 bskyvision.com/163
고려대 김성범 교수님 유튜브 www.youtube.com/channel/UCueLU1pCvFlM8Y8sth7a6RQ/videos
'AI > Machine Learning' 카테고리의 다른 글
| Regularization (0) | 2021.02.19 |
|---|---|
| Random Forest (0) | 2021.02.19 |
| Overfitting (과적합) (0) | 2021.02.17 |
| Decision Tree (0) | 2021.01.21 |
| k-NN (Nearest Neighbors) (0) | 2021.01.18 |
