Random Forest (결정트리)
1) 개요
- decision tree의 ensemble로 decision tree들의 예측을 종합한다.
- decision tree의 low computational complexity (모델 구축 속도), nonparametric 특성으로 base 모델로 사용된다.
- 고차원 데이터에서 변수선택기법으로 널리 활용된다.
모수 : 새로운 데이터 포인트를 분류할 수 있는 함수를 학습하기 위해 훈련 데이터셋에서 모델 파라미터를 예측
정규성을 갖는다는 모수적 특성 이용 (분산, 기대값, 표준편차 등)
(linear regression, linear SVM, logistic regression)비모수 : 고정된 개수의 파라미터로 설명할 수 없다. 훈련 데이터가 늘어나면 파라미터 개수도 늘어난다.
(decision tree, kernel SVM)
2) 특성
- 개별 tree는 과적합 될 수 있다.
- tree 수가 충분히 많을 때, strong law of large numbers에 의해 과적합 되지 않고 에러는 limiting value에 수렴된다.
- Generalization error의 upper bound가 작을수록 좋다.
- 아래의 p 는 개별 tree 간의 상관관계이고 s는 올바르게 예측을 한 tree와 틀린 예측을 한 tree 수 차이의 평균으로 개별 tree간 독립적으로 하던지 개별 tree의 정확도를 높여서 random forest의 성능 높인다.
$$Generalization\:error\leq \frac{\overline{p}(1-s^{2})}{s^{2}}$$
3) 장점
- 앙상블 모델이 개별 decision tree가 만드는 잡음으로부터 안정되어 random forest는 가지치기할 필요가 없다.
- 튜닝할 hyper-parameter가 k (만들 트리 개수)말고는 없다. (k가 높을수록 계산 비용은 증가하지만 성능은 좋다.)
4) 단계별 요약
- n개의 랜덤한 bootstrap sample 추출 (훈련 데이터셋에서 중복을 허용하면서 랜덤한 n개를 뽑는다.)
- 추출한 bootstrap sample에서 decision tree 학습을 시행한다. (중복 허용 x, 랜덤하게 d개의 특성 선택하여 목적함수를 기준으로 노드를 분할)
- 위의 두 단계를 k번 반복
- k개의 예측 결과를 모아 aggregating으로 class label 할당
5) 핵심 아이디어 : Diversity, Random 확보
- 여러 개의 training data를 생성하여 각 데이터마다 개별 decision tree 구축 (bagging)
- decision tree 모델 구축 시 변수 무작위 선택 (Random subspace)
중요변수선택
- 개별 변수가 통계적으로 얼마나 유의한지 정보를 제공하지 않음
- 다음 3가지의 간접적인 방식으로 중요도 결정
1) 원래 데이터셋에 대해 Out of bag(OOB)Error 구함
2) 특정 변수의 값을 임의로 뒤섞은 데이터셋에 대해 OOB Error 구함
3) 개별 변수의 중요도는 2, 1단계 OOB Error 차이의 평균과 분산을 고려하여 결정
Out of bag(OOB) : bootstrap sampling 했을 경우, 뽑아낸 데이터셋에 포함되지 않은 데이터로 테스트 데이터로 사용한다는 개념
4) 수학적 이해
- 개별 tree에 대한 OOB error를 계산 (ri)
- 특정변수의 값을 임의로 섞은 데이터셋에 대해 OOB error 계산 (ei)
- 두 OOB 간의 차이를 구하고 해당 차이의 평균과 분산을 구한다.
$$d_{i} = e_{i} - r_{i},\; i=1,2,\cdots, t$$
$$\overline{d}=\frac{1}{t}\sum_{i=1}^{t}d_{i}\;\; :\;mean$$
$$S_{d}^{2} = \frac{1}{t-1}\sum_{i=1}^{t}(d_{i}-\overline{d})^{2}\;\;:\; variance$$
- d bar값이 크다 -> 해당 변수 값이 매우 중요하다
- xi 변수 중요도
$$v_{i} = \frac{\overline{d}}{S_{d}}$$
코드 예시
1) hyper parameter
- decision tree의 수 (strong law of large numbers를 만족하기 위해 2000개 이상의 decision tree 필요)
- 노드 분할 시 무작위로 선택되는 변수의 수 (classification : sqrt 변수의 수, regression : 변수의 수 /3)
2) 예시 (classification & feature importance)
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators = 150, max_depth = 8, min_samples_leaf = 4,
max_features = 0.2, n_jobs = -1, random_state = 0)
# train
rf.fit(x_train, y_train)
# feature importance
y = rf.feature_importances_
x = x_train.columns.values
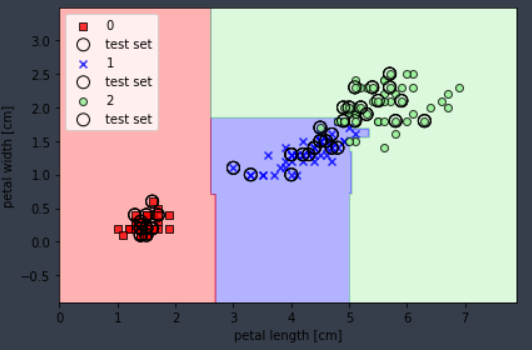
참고
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 (길벗)
고려대 김성범 교수님 유튜브 www.youtube.com/channel/UCueLU1pCvFlM8Y8sth7a6RQ
'AI > Machine Learning' 카테고리의 다른 글
| Model pipeline (0) | 2021.02.22 |
|---|---|
| Regularization (0) | 2021.02.19 |
| Support Vector Machine; SVM (0) | 2021.02.18 |
| Overfitting (과적합) (0) | 2021.02.17 |
| Decision Tree (0) | 2021.01.21 |
