개념
1) 패턴을 변수의 조합으로 나타냄
2) 스무고개와 유사함 (yes or no)
개요
1) 데이터가 균일해지도록 2개 이상으로 분할
- 분류 : 비슷한 범주 기준
- 예측 : 비슷한 수치 기준
2) 이진분할에 의해서 끝마디의 분할된 데이터의 개수는 input개수와 동일하다.
3차원에서의 모형

예측 모델
1) 새로운 입력 데이터 (Xnew)에 대한 예측값 (Ynew)은 Xnew가 속하는 끝 노드 y값들의 평균값이 된다. (오류가 최소)
2) 과정
- 데이터를 m개로 분할

- cost function이 최소가 되도록 분할

3) 분할변수와 분할점 결정 방법
- 모든 분할변수와 분할점 경우의 수를 계산하며, cost function이 최소가 되는 순서로 노드를 생성한다.
- 그리디 알고리즘과 맥락이 같다.
분류 모델
1) 데이터 마다 k개의 클래스 존재 (범주)
2) Rm : 끝 노드 m에 해당하며 Nm 데이터 개수를 가지고 있다.
3) p hat mk : 끝 노드 m에서 k 클래스에 속해 있는 데이터의 비율
i.e. - [1, 1, 1, 2, 2] -> p hat 11 = 3/5, p hat 12 = 2/5
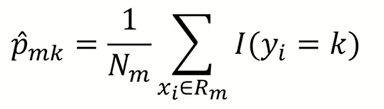
4) 분류된 데이터의 p hat mk 값 (해당 범주의 비율) 중 가장 큰 값에 해당되는 클래스 (k)로 분류

분할법칙
1) 분할변수와 분할점 (j, s)는 데이터의 클래스 (y)의 분포를 잘 구별해주는 쪽으로 정함
2) 분포를 잘 구별해주는 측도로 불순도를 정의한다.
i.e. 분류 후, (0, 1)의 비율이 (45, 55) > (90, 10) 에 비해 불순도가 높다고 해석
분류 모델 비용함수 (불순도 측정)
- 개요 : 예측모델과 다르게 cost function함수로 설명하는 것은 무의미 대표적으로 3 가지의 방식을 통해 측정한다.
1) Misclassification rate
- 실제 클래스 (yi)와 예측한 클래스 (k(m))가 매칭되지 않은 것을 최소화
- 아래의 두 지표와 달리 미분이 불가능하여 자주 사용되지 않음

2) Gini index
$$G.I(A)=\sum _{ i=1 }^{ d }{ { \left( { R }_{ i }\left( 1-\sum _{ k=1 }^{ m }{ { p }_{ ik }^{ 2 } } \right) \right) } }$$
- 데이터의 분산정도를 정량화해서 표현
3) Cross-entropy
$$Entropy(A)=-\sum _{ k=1 }^{ m }{ { p }_{ k }\log _{ 2 }{ { (p }_{ k }) } }$$
$$Entropy[9+, 5-]=-\frac { 9 }{ 14 } \log _{ 2 }{ (\frac { 9 }{ 14 } ) } -\frac { 5 }{ 14 } \log _{ 2 }{ (\frac { 5 }{ 14 } ) } \approx 0.94$$
- 분기 전과 후의 엔트로피를 비교하여 엔트로피가 감소하는 방향으로 학습 진행
- Information gain (IG)
: 특정 변수를 사용했을 때, entropy 감소량
: 각 변수(속성)에 따라 분기를 진행했을때, 가장 entropy가 크게 감소하는 변수를 선택하여 다음 분기로 나아감

단점
1) 계층적 구조로 에러가 발생하면 다음 노드로 에러가 전파된다.
2) 학습 데이터의 미세한 변화에 민감하다.
3) 최종 노드 개수가 지나치게 크다면 과적합 위험이 있다.
--> 단점 보완을 위해 Random forest 사용
코드 예시
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='gini', max_depth = 4, random_state = 1)
tree.fit(X_train, y_train)
김성범 교수님의 강의를 정리하였습니다. www.youtube.com/watch?v=W-DNu8nardo
'AI > Machine Learning' 카테고리의 다른 글
| Random Forest (0) | 2021.02.19 |
|---|---|
| Support Vector Machine; SVM (0) | 2021.02.18 |
| Overfitting (과적합) (0) | 2021.02.17 |
| k-NN (Nearest Neighbors) (0) | 2021.01.18 |
| 주성분 분석 (PCA) (0) | 2021.01.04 |
