Bias-Variance Trade-off
1) 개요
- 아래의 이미지를 통해 bias와 variance의 직관적인 이해를 할 수 있다.
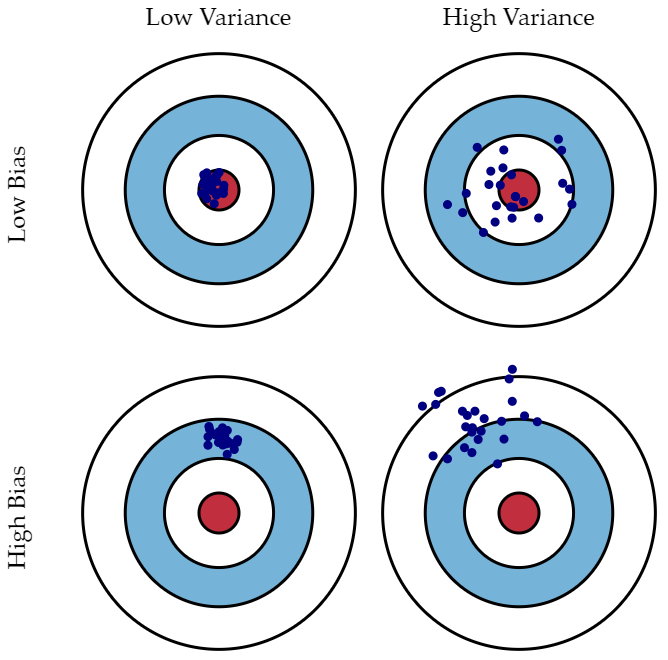
2) Bias (편향)
- high bias, low variance일 경우, 모델이 단순하여 underfitting을 초래하고 train, test dataset 모두에서 낮은 정확도를 나타낼 수 있다.
3) Variance (분산)
- low bias, high variance일 경우, 모델이 너무 복잡하여 overfitting을 초래하여 train dataset에서는 높은 정확도를 보이지만 새로운 data에 대한 정확도는 현저히 낮다.
4) 수학적 이해
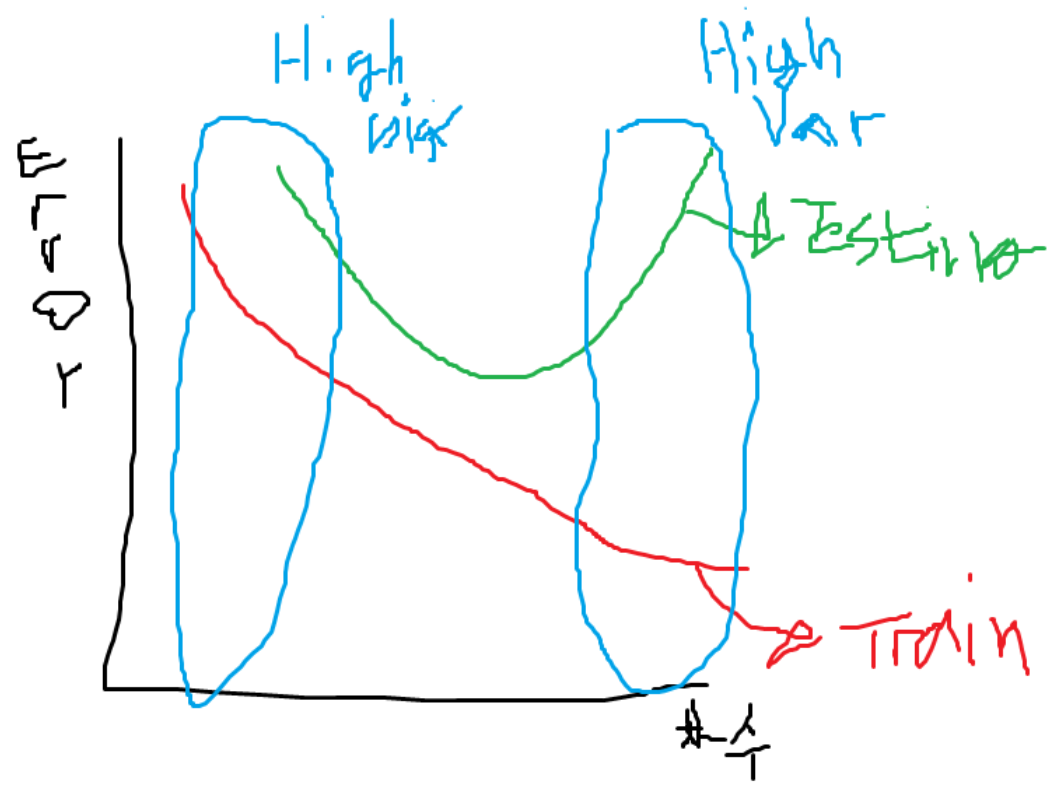
- expected MSE (mean squared error)를 낮추기 위해 bias 또는 var를 낮춰야 성능이 좋아진다.

Least squares method (최소제곱법) : MSE를 최소화하는 회귀계수를 계산
- 파라미터를 데이터의 함수꼴로 나옴)
- 선형회귀 모델로부터 나온 값의 차이의 제곱의 합을 최소로하는 계수를 찾는다.
- convex 형태여서 미분하고 0으로 만들고 연립방정식을 통해 우항이 나온다.
$$argmin(\sum_{i=1}^{n}((y_{i}-x_{i}\beta)^{2})) = (X^{T}X)^{-1}X^{T}y$$
Regularization model
1) 개요
- bais와 var가 동시에 낮은 모델은 없기 때문에 bias를 추가하여 모델을 간단하게 만들어 var을 줄인다.
- 가중치를 제한하여 훈련 데이터셋에 대한 의존성을 줄여준다.
- 목표는 규제가 없는 비용과 페널티항의 합을 최소화하는 것
- 최소제곱법과 다르게 회귀계수에 제약(= 가중치 w)을 더한다.
2) Ridge Regression (L2-norm regularization)
- 제곱 오차를 최소화하면서 회귀 계수 beta의 L2-norm을 제한 (beta의 제곱의 합)
$$L(\beta) = min \sum_{i=1} (y_{i} - \hat{y}_{i})^{2} + \lambda \sum_{j=1}^{p}\beta_{j}^{2}$$
- 뒷부분은 generalization accuracy로써 parameter lambda를 조절하여 tradeoff를 조절한다.
- 아래의 그림에서 회색 원 바깥으로 나가지 못하도록 막는 역할을 하는 것이다.
- 규제 파라미터 lambda값이 커질수록 패널티 비용이 증가하여 회색공이 작아진다.
$$\hat{\beta}^{ridge} = (X^{T}X + \lambda I_{p})^{-1}X^{T}y$$

3) Lasso; least absolute shrinkage and selection operator (L1-norm regularization)
- 변수 선택 가능하며 회귀 계수 beta의 L1-norm을 제한 (beta의 절대값의 합)
$$L(\beta) = min \sum_{i=1} (y_{i} - \hat{y}_{i})^{2} + \lambda \sum_{j=1}^{p}|\beta_{j}|$$
- 아래의 그림에서 볼 수 있듯이 해당 지점에서 특정 변수의 계수 값은 0이다. 따라서 해당 변수는 예측에 아무런 영향을 끼치지 못한다는 말이다. 이는 중요하지 않은 변수라고 할 수 있다. (변수 선택 가능)
- L1-norm은 미분이 불가능하여 ridge와 달리 closed form solution을 구할 수 없다.

| Ridge (L2) | Lasso (L1) |
| 변수 선택 불가능 | 변수 선택 가능 |
| Closed form solution 존재 (미분 가능) | Closed form solution 존재 x (numerical optimization 이용) |
| 변수 간 상관관계가 높은 상황에서 좋은 성능 | 변수 간 상관관계가 높을 때 ridge에 비해 성능 저하 |
| 크기가 큰 변수를 우선적으로 줄이는 경향이 있음 |
4) Elastic Net
- Ridge + Lasso (L1 and L2 regularization)
- ridge는 가중치가 0이 안되기 때문에 변수가 많으면 여전히 복잡하고 lasso는 정보의 손실로 인해 성능이 낮아질 수도 있다. 이를 해결하기 위해 사용한다.
- 상관관계가 큰 변수를 동시에 선택/배제하는 특성을 지니고 있다.
$$\hat{\beta}^{enet}= argmin(\sum_{i=1}^{n}(y_{i}-x_{i}\beta^{2})+ \lambda_{1} \sum_{j=1}^{p}|\beta_{j}|+ \lambda_{2} \sum_{j=1}^{p}\beta_{j}^{2})$$
코드 예시
# Ridge regression
from sklearn.linear_model import Ridge
rid = Ridge(alpha = 0.05, normalize = True)
rid.fit(x_train, y_train)
# Lasso regression
from sklearn.linear_model import Lasso
ls = Lasso(alpha = 0.3, normalize = True)
ls.fit(x_train, y_train)
# Elastic Net regression
from sklearn.linear_model import ElasticNet
# alpha = a + b -> a : L1, b : L2
EN = ElasticNet(alpha = 1, l1_ratio = 0.5, normalize = False)
EN.fit(x_train, y_train)
# Use L1, L2, ElasticNet for regression algorithm
from sklearn.linear_model import LogisticRegression
# penalty default : l2 (l1, ElasticNet available)
# C : inverse of regularization
lr = LogisticRegression(solver = 'liblinear',
multi_class = 'auto',
penalty = 'l1',
C=1.0,
random_state = 42)
lr.fit(X_train_std, y_train)1) 가중치 변화 예시
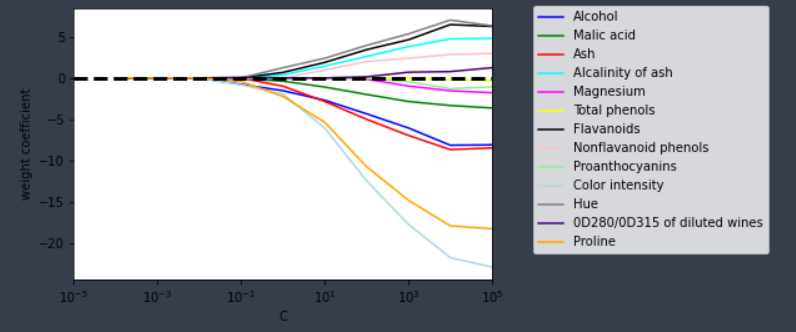
참고
www.youtube.com/channel/UCueLU1pCvFlM8Y8sth7a6RQ
머신러닝 교과서 (길벗)
rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear/
'AI > Machine Learning' 카테고리의 다른 글
| Validation (Cross-val, learning-curve, GridSearch) (0) | 2021.02.23 |
|---|---|
| Model pipeline (0) | 2021.02.22 |
| Random Forest (0) | 2021.02.19 |
| Support Vector Machine; SVM (0) | 2021.02.18 |
| Overfitting (과적합) (0) | 2021.02.17 |
