
Abstract
SENet은 2017년 ILSVRC에서 우승을 차지한 모델이다. 여기서 Squeeze-and-Excitation (SE) block을 제시하였다. 이를 사용하여 채널 간의 상호 관계를 모델링하면서 channel-wise feature를 조정할 수 있다. 어떤 모델에도 적용할 수 있으며 성능을 향상시키면서 parameter의 수가 많이 늘지 않기 때문에 연산량의 증가가 크지 않다.
Introduction
CNN network에서 conv filter는 local receptive fields에서 spatial과 channel-wise information을 합쳐 이웃 픽셀 간의 상호 연관성을 학습한다. non-linear activation function이나 downsampling operators(pooling)을 사용하여 계층적 패턴을 찾아내고 global theoretical receptive fields를 달성하기도 한다.
저자는 Squeeze-and-Excitation (SE) 방법을 적용해 feature recalibration을 수행하여 중요한 feature는 강조하고 그렇지 않은 feature는 억제할 수 있다고 한다. 장점으로는 아래와 같다.
- SE block은 매우 간단하여 다른 architecture에 붙여 사용할 수 있다.
- 연산량에 있어서 매우 가볍기 때문에 모델의 복잡성이 조금 밖에 올라가지 않는다.
Squeeze-and-Excitation Blocks

$$F_{tr}(X)=U, \;\;\; X\in R^{H'\times W' \times C'},\: U\in R^{H\times W \times C}$$
F_tr은 conv layer로 input X를 U로 변환해준다. F_tr은 learned set of filter kernels인 V를 사용한다. V에서 c는 몇번째 filter인 것을 의미한다. 그리고 U도 filter의 개수가 동일한 값이 나오기 때문에 최종적으로 아래와 같이 나타낼 수 있다.
$$u_{c} = v_{c} * X = \sum_{s=1}^{C'}v_{c}^{s}*x^{s}, \;\;V = [v_{1}, v_{2}, ..., v_{C}],\: U = [u_{1}, u_{2}, ..., u_{C}]$$
위의 변환을 통해 채널 상호 의존성을 높여서 informative feature에 대해 네트워크가 더욱 민감하게 반응할 것으로 기대한다.
1) Squeeze : Global Information Embedding
local receptive field의 filter들은 해당 region 외에는 정보를 추출할 수가 없다. 따라서 global spatial information을 channel descriptor로 squeeze한다. channel 단위로 통계를 내기 위해 global average pooling을 사용한다. c-th element of z는 아래와 같이 연산한다.
$$z_{c} = F_{sq}(u_{c}) = \frac{1}{H \times W}\sum_{i=1}^{H}\sum_{j=1}^{W}u_{c}(i, j)$$
HxWxC 크기의 feature map을 1x1xC 크기로 만든 것이다. 저자는 global average pooling외에도 다른 방법을 사용해도 된다고 한다.
2) Excitation: Adaptive Recalibration
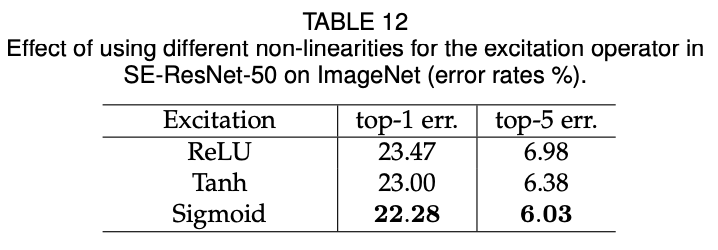
squeeze 연산 이후에 recalibration을 통해 channel-wise dependencies를 계산한다. 채널 간의 의존성을 찾기 위해 사용되는 function에는 2가지 조건이 있다.
- it must be flexible (capable of learning a nonlinear interaction between channels)
- it must learn a non-mutually- exclusive relationship (2개 이상의 channel이 동시에 강조가능해야 하기 때문)
위의 조건에 따라 저자는 sigmoid activation을 사용했다. \delta는 ReLU이다.
$$s = F_{ex}(z, W) = \sigma(g(z, W)) = \sigma(W_{2}\delta(W_{1}z)),\;\; W_{1}\in R^{\frac{C}{r}\times C},\: W_{2}\in R^{C \times \frac{C}{r}}$$
모델의 복잡도를 줄이고 대표성을 주기 위해 ReLU 함수 전후로 FC layers 두 개를 사용하여 bottleneck을 구성한다. r은 reduction ratio로 W_1에서는 노드 수를 줄이고 W_2에서는 다시 증가시킨다. SE block의 최종 output은 U를 s로 rescaling한다.
$$\tilde{x}_{c} = F_{scale}(u_{c}, s_{c}) = s_{c}u_{c}, \;\; \tilde{X} = [\tilde{X}_{1},\tilde{X}_{2}, ..., \tilde{X}_{C}]$$
scalar s_c로 channel-wise multiplication을 수행하여 채널들의 중요도에 따라 scale된다.
3) Instantiations
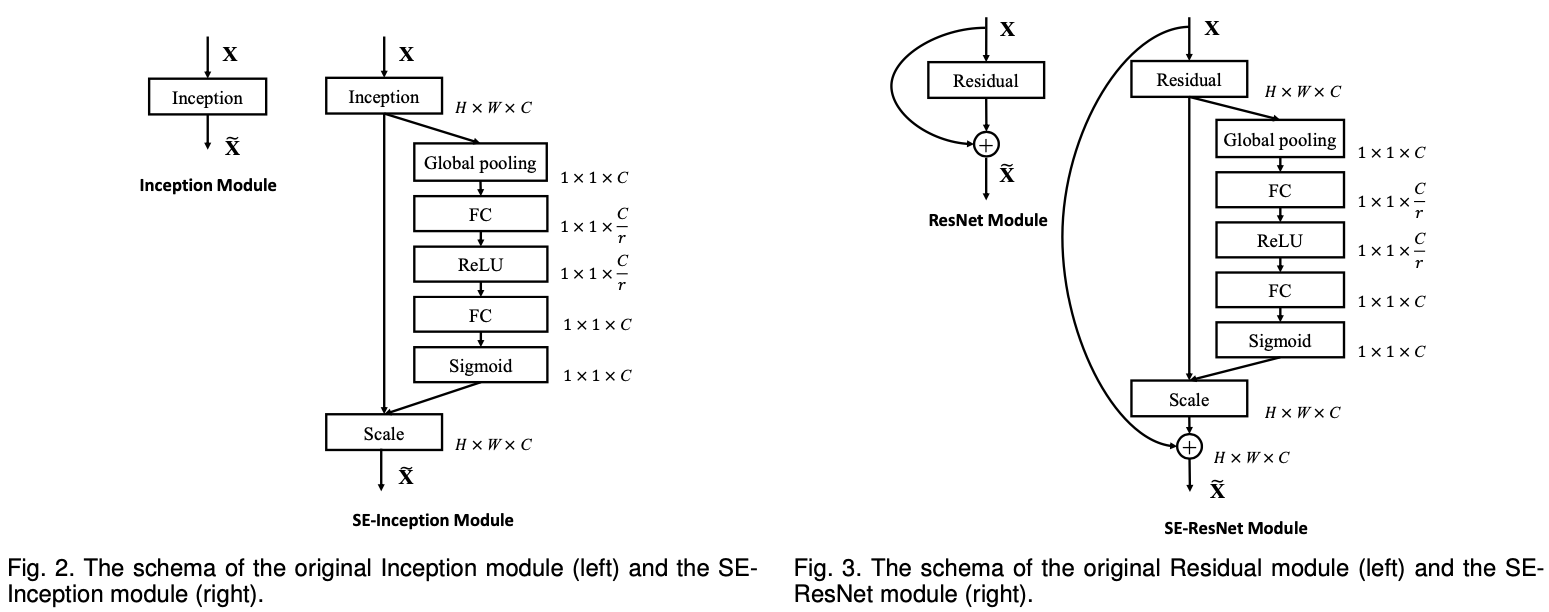
VGGNet과 같은 기본적인 architectures에서는 각 convolution non-linearity 뒤에 적용이 가능하다. 그 외에 Resnet이나 GoogLeNet같은 경우는 위와 같이 적용할 수 있다. 이를 통해, SE block의 flexibility를 알 수 있다.
Model and Computational Complexity

SE block을 적용함으로써 정확도가 올라가지만 모델의 복잡도가 올라가게 된다. 하지만 ResNet-50과 SE-ResNet-50의 복잡도를 비교했다. 0.26% 밖에 복잡도가 올라가지 않았지만 정확도는 ResNet-101과 비슷했다고 한다.
계산복잡도에 영향을 끼치는 변수로 SE block내 FC layer의 reduction ratio r이다. 이때 추가되는 weight parameter 개수는 아래의 수식을 통해 구할 수 있다.
$$\frac{2}{r}\sum_{s=1}^{S}N_{s}\cdot C_{s}^{2}$$
S는 number of stages이고 C_s는 output channel의 dimension, N_s는 stage S내에서 반복되는 block의 개수이다.
Experiments

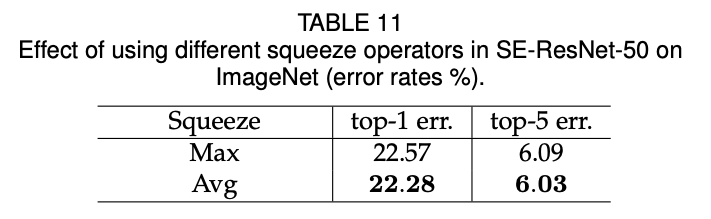
1) Effect of Squeeze
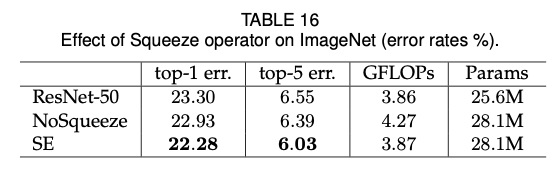
squeeze가 SE block 내에서 중요한 역할을 하는지 평가하기 위해 기존의 ResNet-50, SE-ResNet-50과 squeeze (global average pooling)연산을 실시하지 않고 parameter 수만 동일하게 맞춘 것으로 나눠 실험했다. 결과적으로 NoSqueeze에서는 global embedding을 실시하지 않았기 때문에 실시 여부에 따라 모델의 성능에 크게 영향을 미쳤다.
2) Effect of Excitation

SE block에서 excitation의 기능을 시각적으로 보여주기 위해 연구를 진행했다. SE-ResNet-50 모델의 activation example에 대해 연구하고 network에서 다양한 depth 상에서 다른 classes와 input images들에 대한 distribution을 실험했다.
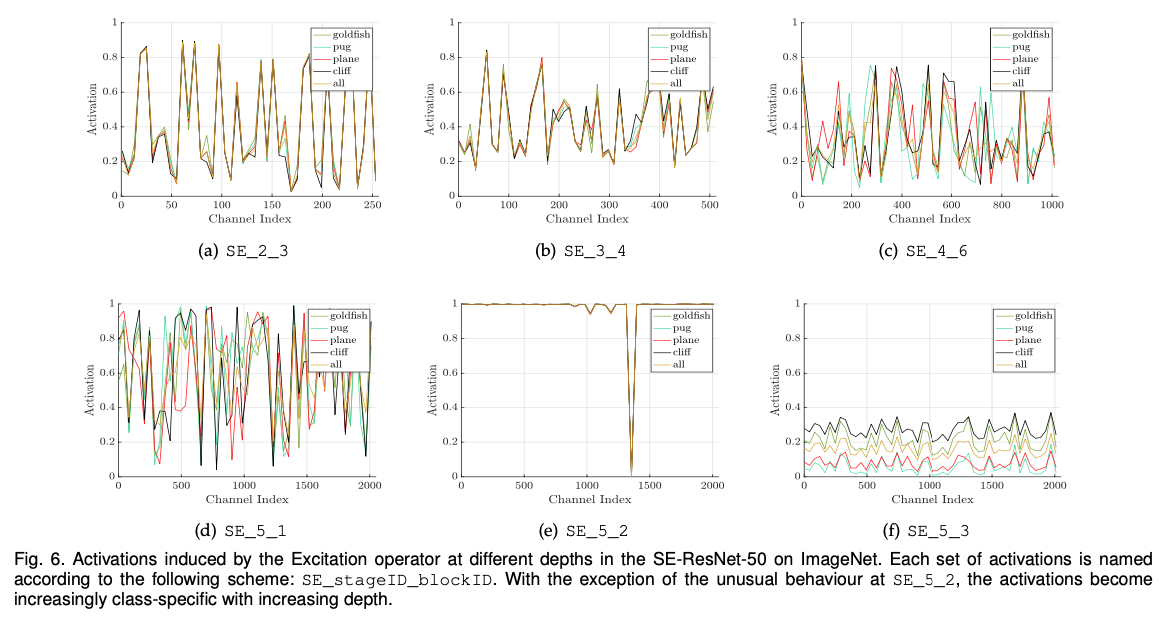
- 네트워크 초반부의 layer에서는 다른 class에 걸친 distribution이 매우 유사하다.
- 깊이가 깊어질수록 각 channel의 value는 class간의 구분이 가능할정도로 분포의 차이가 난다.
- 더욱 깊어지면 class별 유사한 분포를 보여주기 때문에 이에 해당되는 SE block은 제거한다.
'AI > Paper' 카테고리의 다른 글
| Video Transformer Network (2021) 리뷰 (0) | 2021.04.30 |
|---|---|
| MoViNets: Mobile Video Networks for Efficient Video Recognition (2021) 리뷰 (0) | 2021.04.26 |
| Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset (2017) (0) | 2021.04.18 |
| Skeleton Aware Multi-modal Sign Language Recognition (2021) (0) | 2021.04.13 |
| Deep residual learning for image recognition; ResNet (2015) (0) | 2021.03.29 |
