Logistic regression
1) 개요
- 새로운 관측치를 기존 범주 중 하나로 예측 (범주예측, 분류)
2) 이론 배경
- X값이 주어졌을 때 출력변수 Y가 1의 값을 가질 확률
$$Y_{i} = \beta_{0} + \beta_{1}X_{i} + \varepsilon_{i}\;\; Y_{i} = 0\:or\:1$$
$$Assume\: E(\varepsilon_{i}) = 0,\;\;\; E(Y_{i}) = \beta_{0} + \beta_{1}X_{i}$$
$$P(Y_{i} = 1) = \pi_{i}\;,\;\;P(Y_{i} = 0) = 1- \pi_{i}$$
$$E(Y_{i}) = 1\cdot \pi_{i} + 0\cdot (1- \pi_{i})=\pi_{i} $$
$$E(Y_{i}) = \beta_{0} + \beta_{1}X_{i}=\pi_{i}$$
3) Logistic function (sigmoid function)
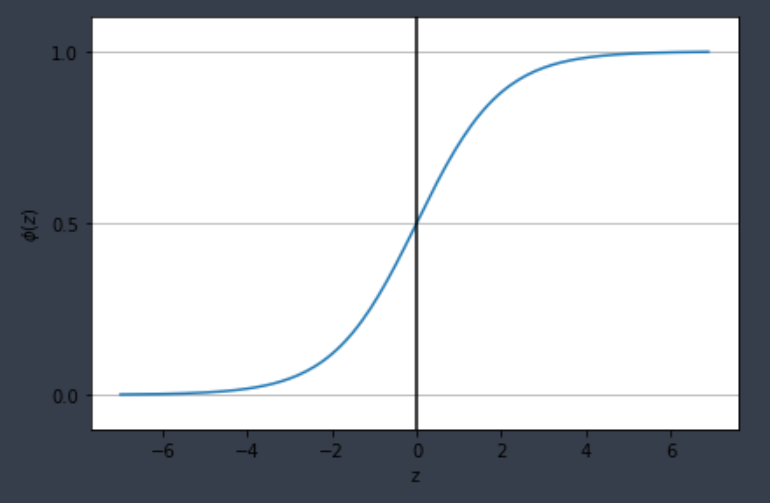
- Output range : 0 ~ 1 (pdf 요건을 충족)
- 인풋값에 대해 단조증가(단조감소)함수
- 미분결과를 아웃풋의 함수로 표현 가능 (경사하강법에 매우 유용)
$$\frac{d\phi(z)}{dz} = \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}}) = \phi(z)(1-\phi(z))$$
ex) input X가 1개인 로지스틱 모델 예 (관측치 x가 범주 1에 속할 확률)
$$E(y) = \pi(X=x)=\frac{1}{1+e^{-(\beta_{0}+\beta_{1}x)}}$$
Odds (승산)
1) 개요
- 성공 확률을 p로 정의할 때, 실패(범주 0에 속할 확률) 대비 성공(범주 1에 속할 확률) 비율
$$Odd = \frac{p}{1-p}$$
$$p=1 \;\Rightarrow \; odd=\infty$$
$$p=0 \;\Rightarrow \; odd=0$$
2) Logit Transform
- Odd에 log를 취하면 선형식이 나와서 직관적 해석이 가능
$$\pi(X=x)=\frac{1}{1+e^{-(\beta_{0} + \beta_{1}x)}}$$
$$Odds=\frac{\pi(X=x)}{1-\pi(X=x)}$$
$$log(Odds)=log(\frac{\pi(X=x)}{1-\pi(X=x)})=\beta_{0}+\beta_{1}x$$
Logistic regression의 parameter 추정
1) Maximum likelihood estimation (최대 우도 추정법)
$$lnL=\sum_{i}y_{i}(\beta_{0} + \beta_{1}X_{1}+\cdots+\beta_{p}X_{p})+\sum_{i}ln(1+e^{\beta_{0} + \beta_{1}X_{1}+\cdots+\beta_{p}X_{p}})$$
- 위의 log likelihood function이 최대가 되는 파라미터 beta 결정
- log likelihood function은 파라미터 beta에 대해 비선형이므로 선형회귀 모델과 같이 명시적인 해가 없음
- 수치 최적화 알고리즘을 이용하여 해를 구함
코드 예시
class LogisticRegressionGD(object):
'''
w_ : 1d-array, 학습된 가중치
cost_ : 에포크마다 누적된 비용 함수 값
'''
def __init__(self, eta = 0.05, n_iter = 100, random_state = 1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc = 0.0, scale = 0.01,
size = 1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = y - output
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (-y.dot(np.log(output)) -
((1 - y).dot(np.log(1 - output))))
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, z):
return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
def predict(self, X):
return np.where(self.net_input(X) >= 0.0, 1, 0)
# --------------------------------------------------
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver = 'liblinear', multi_class = 'auto',
C = 100.0, random_state = 1)
lr.fit(X_train_std, y_train)참고
머신러닝 교과서 (길벗)
고려대 김성범 교수님 유튜브 www.youtube.com/channel/UCueLU1pCvFlM8Y8sth7a6RQ/videos
'AI > Machine Learning' 카테고리의 다른 글
| Clustering Analysis (0) | 2021.02.28 |
|---|---|
| Linear regression (0) | 2021.02.26 |
| Ensemble (Voting, Bagging, Boosting) (0) | 2021.02.24 |
| Model evaluation metrics (0) | 2021.02.23 |
| Validation (Cross-val, learning-curve, GridSearch) (0) | 2021.02.23 |
