Linear regression
1) 개요
- 하나 이상의 특성 (X)과 연속적인 타킷변수 (y)사이의 선형결합으로 모델링
- 지도 학습의 하위 범주 중 하나로 분류와 달리 연속적인 출력 값을 예측
$$Y = \beta_{0} + \beta_{1}X$$
2) 선형회귀 모델 가정
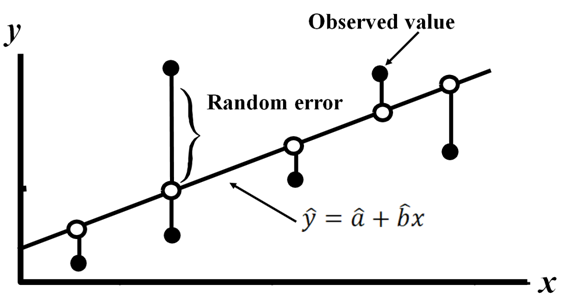
- 확률오차 (random error)는 정규분포를 따르고 평균이 0, 분산이 sigma^2이다.
$$\varepsilon \sim N(0,\sigma^{2}),\: i=1,2,...,n$$
- 입력변수 (X)와 출력변수 (Y) 평균과의 관계를 설명하는 선형식을 찾는다.
- 가지고 있는 데이터들의 함수식으로 parameter (개요의 beta)를 추정한다.
Residual (잔차)
- 잔차는 확률오차가 실제로 구현된 값으로 같지 않다.
$$e=y-\hat{y}$$
3) Least squares estimation algorithm (최소제곱법; 파라미터 추정 알고리즘)
- 비용함수 (random error들의 제곱의 합)가 최소가 되도록 만든다.
$$\sum_{i=1}^{n}(Y_{i} - (\beta_{0} + \beta_{1}X_{i}))^{2}$$
$$min_{\beta} \sum_{i=1}^{n}(Y_{i} - (\beta_{0} + \beta_{1}X_{i}))^{2}$$
- convex 형태여서 전역 최소 기울기를 구하기 위해 편미분을 취해준다.
$$\frac{\partial C (\beta_{0},\beta_{1})}{\partial \beta_{0}}=-2\sum_{i=1}^{n}Y_{i} -(\beta_{0} + \beta_{1}X_{i})=0$$
$$\frac{\partial C (\beta_{0},\beta_{1})}{\partial \beta_{1}}=-2\sum_{i=1}^{n}Y_{i} -(\beta_{0} + \beta_{1}X_{i})X_{i}=0$$
- 편미분을 취해준 뒤 연립방정식과 동일한 방식으로 해결한다.
$$\therefore \hat{\beta}_{0} = \bar{Y}-\hat{\beta}_{1}\bar{X},\;\; \hat{\beta}_{1}=\frac{\sum_{i=1}^{n}(X_{i}-\hat{X})(Y_{i}-\hat{Y})}{\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}$$
class LinearRegressionGD(object):
def __init__(self, eta = 0.001, n_iter = 20):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() /2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return self.net_input(X)
# -----------------------------------------------------
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
print('기울기: ', slr.coef_[0])
print('절편: ', slr.intercept_)
선형 회귀 모델 성능 평가
1) MSE (Mean Squared Error; 평균제곱오차)
- SSE를 샘플 개수로 나눈 것
$$SSE = \sum_{i=1}^{n}(Y_{i}-\hat{Y})^{2}$$
$$MSE = \frac{1}{n}\sum_{i=1}^{n}(Y_{i}-\hat{Y})^{2}$$
from sklearn.metrics import mean_squared_error
print(f"훈련 : {round(mean_squared_error(y_train, y_train_pred), 3)}")
print(f"테스트 : {round(mean_squared_error(y_test, y_test_pred), 3)}")
2) 결정계수 (Coefficient of Determination: R^2)
- 모델 성능을 잘 해석하기 위해 만든 MSE의 표준화된 버전
- 사용하고 있는 X변수가 Y변수의 분산을 얼마나 줄였는지 정도
- 사용하고 있는 X변수의 품질

$$R^{2} = 1-\frac{SSE}{SST}$$
- R^2는 0과 1 사이에 존재
- R^2 = 1 -> 모든 관측치가 회귀직선 위에 있다.
- R^2 = 0 -> 모든 관측치가 회귀직전 위에 있지 않다.
from sklearn.metrics import r2_score
print(f"훈련 : {round(r2_score(y_train, y_train_pred), 3)}")
print(f"테스트 : {round(r2_score(y_test, y_test_pred), 3)}")
Polynomial regression (다항 회귀)
1) 개요
- 두 개 이상의 독립변수가 있는 다중 회귀와 다르게 다항 회귀는 동일 독립 변수의 차수를 높인다.
- 비선형 관계를 모델링하는 것이지만 다변량 선형 회귀모델로 생각할 수도 있다.
- 다만, 극단적으로 차수를 높이면 overfitting 문제가 있을 수 있다.
- 일반적으로 p value가 0.05 이하일 경우 일때만 차수를 높인다.
from sklearn.preprocessing import PolynomialFeatures
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)참고
고려대 김성범 교수님 유튜브www.youtube.com/channel/UCueLU1pCvFlM8Y8sth7a6RQ/videos
머신러닝 교과서 (길벗)
'AI > Machine Learning' 카테고리의 다른 글
| Logistic regression (0) | 2021.03.02 |
|---|---|
| Clustering Analysis (0) | 2021.02.28 |
| Ensemble (Voting, Bagging, Boosting) (0) | 2021.02.24 |
| Model evaluation metrics (0) | 2021.02.23 |
| Validation (Cross-val, learning-curve, GridSearch) (0) | 2021.02.23 |
