Image filtering (Detecting edges)

Image derivatives

1) 개요

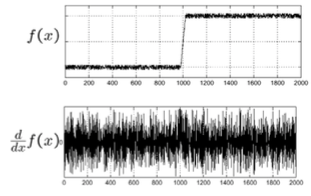
    - Intuitively, the edges should have rapid change. By using Gaussian blurring, remove the noises first. The above image is the dreivative without applying Gaussian blurring.

ref : http://www.cs.cmu.edu/~16385/lectures/lecture2.pdf

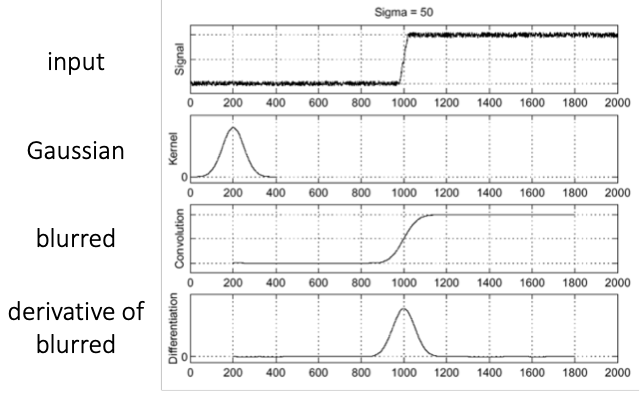
    - Intensity changes over the image is important information.

    - x and y derivatives of grayscale image can describe the intensity change.

    - By gradient, get vector value from the image and can effectively use for edge detection.

 

2) Basic computation

    - the image is in cumulative space. Its derivative is doing convolution using [-1, 1].

    - After generate a matrix to compute the derivatives, do dot product with image matrix.

    - Below tables are sample of computing the matrix.

Original grayscaled image

    - x derivatives compute by right side.

X derivatives

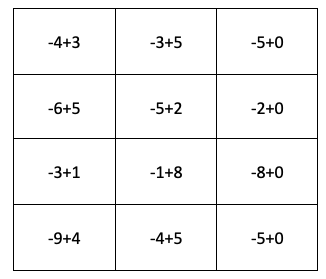
    - y derivatives compute by down side.

Y derivatives

 

3) Gradient magnitude and angle

    - By using image gradient vector, we can get gradient magnitude and angle.

    - gradient magnitude : describe how strong the image intensity change

$$\nabla I = \sqrt{I_{x}^{2} + I_{y}^{2}}$$

    - angle (direction) : indicates direction of largest intensity change at each point (pixel)

$$\alpha (x, y) = arctan2(I_{y}, I_{x})$$

 

Gradient Filter

1) 개요

    - There are various kinds of gradient filters. (High-pass filters; HPF)

    - On behalf of a basic computation above, we can simply implement deriviates.

    - It is critical to blur first.

 

2) Sobel

    - Basic filter to extract edge from the images.

    - Mostly, use with Gaussian smoothing.

    - It relatively standardize projected pixel to extract brightness rate of change. So, strong to a noise.

 

3) Prewitt

 

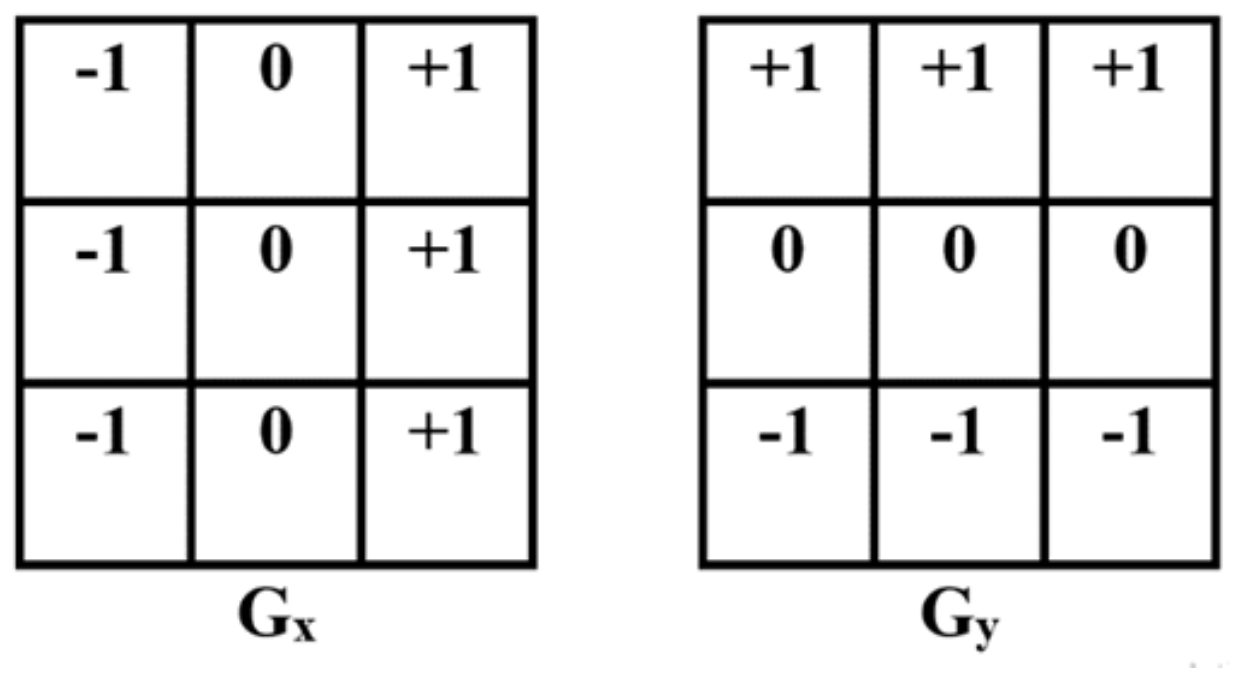
4) DoG filter (Derivative of Gaussian)

$$\frac{\partial}{\partial x} (h*f) = (\frac{\partial}{\partial x}h)*f$$

ref : http://www.cs.cmu.edu/~16385/lectures/lecture2.pdf

 

5) LoG filter (Laplacian of Gaussian)

$$f''(x) = \lim\frac{f(x+h)-2f(x)+f(x-h)}{h^{2}}$$

ref : http://www.cs.cmu.edu/~16385/lectures/lecture2.pdf

 

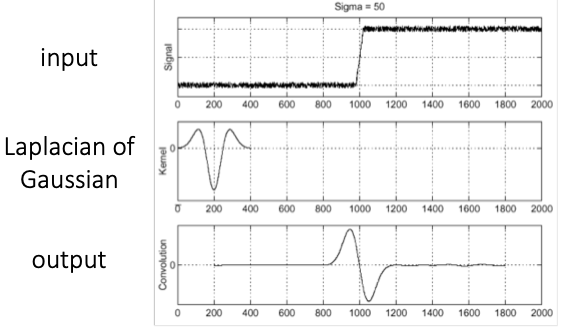
Example

1) Basic

# generate a matrix to compute the derivative in x-direction
Dx = -np.ones((n_col, n_col))
Dx = np.tril(Dx, 0)
Dx = np.triu(Dx, 0)
np.fill_diagonal(Dx[1:, :-1], 1)

# generate a matrix to compute the derivative in x-direction
Dy = -np.ones((n_row, n_row))
Dy = np.tril(Dy, 0)
Dy = np.triu(Dy, 0)
np.fill_diagonal(Dy[:-1, 1:], 1)

# compute the derivative of I with respect to x, y direction
Ix = I.dot(Dx)
Iy = Dy.dot(I)

# gradient magnitude
norm_gradient = np.square(Ix) + np.square(Iy)

 

2) SciPy (Sobel)

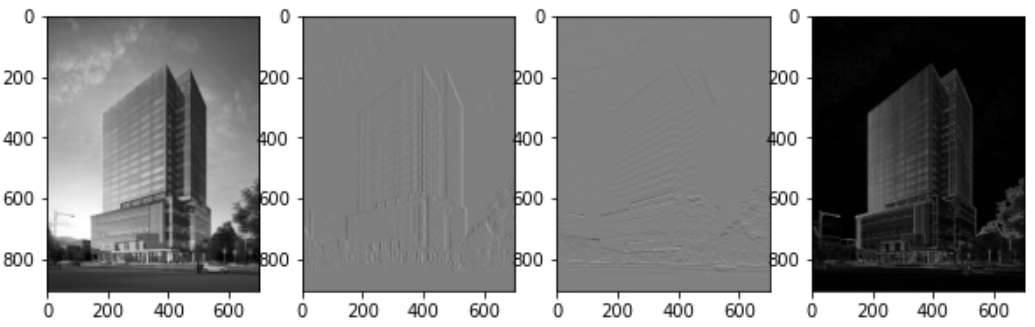
im = np.array(Image.open('/Users/sejongpyo/Downloads/building.jpg').convert('L'))

# Sobel derivative filters
imx = zeros(im.shape)
filters.sobel(im, 1, imx)

imy = zeros(im.shape)
filters.sobel(im, 0, imy)

magnitude = sqrt(imx**2 + imy**2)

f, ax = subplots(1, 4, figsize = (10, 7))
ax[0].imshow(im)
ax[1].imshow(imx)
ax[2].imshow(imy)
ax[3].imshow(magnitude)
plt.show()

 

3) OpenCV

img = cv2.imread('/Users/sejongpyo/downloads/baduk.png')

dst_x = cv2.Sobel(img, ddepth = -1, dx = 1, dy = 0, ksize = -1)
dst_y = cv2.Sobel(img, ddepth = -1, dx = 0, dy = 1, ksize = -1)

---

참고

www.cs.cmu.edu/~16385/lectures/lecture2.pdf

opencv official document

www.ijser.org/researchpaper/Analytical-Comparison-between-Sobel-and-Prewitt-Edge-Detection-Techniques.pdf

yeowool0217.tistory.com/543

http://programmingcomputervision.com/