Kernel method
1) 개요
- 선형적으로 구분이 불가능한 비선형 데이터를 다루는데 사용한다.
- 주로 SVM, LR과 같은 분류 알고리즘에 사용된다.
2) Kernel function
- 벡터 간의 내적 값 (닮음, 유사도)을 구하는 일종의 함수이다.
$$K(\vec{v},\vec{w})\;\;\; K:R^{N}\times R^{N}\: \rightarrow R$$
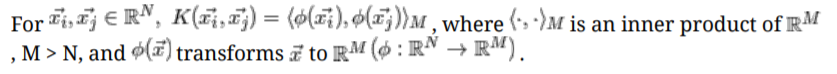
- kernel trick이라고도 불리는 이유는 직접적인 계산으로 차원을 늘리는게 아니라 암묵적으로 추가 메모리 사용없이 늘릴 수 있기 때문이다.
3) Various type of kernels
- Polynomial Kernel
$$K(\vec{v},\vec{w})=(\vec{v}^{T} \vec{w} + \theta)^{P}$$
- Sigmoid Kernel
$$K(\vec{v},\vec{w})=tanh(\eta \vec{v}^{T} \vec{w} + \theta)$$
- RBF; Radial Basis Function Kernel
$$K(\vec{v},\vec{w})=exp(-\frac{||\vec{v}-\vec{w}||^{2}}{2\sigma^{2}})=exp(-\gamma ||\vec{v}-\vec{w}||^{2})$$
Kernel PCA
1) 기본 PCA와 커널 PCA 차이 시각화

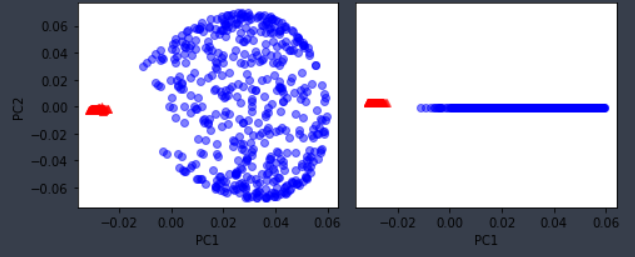
2) 전체 과정 코드 예시
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
'''
hyperparameter
X : {numpy ndarray}, shape = [n_samples, n_features]
gamma : float RBF 커널 튜닝 매개변수
n_components : int 반환할 주성분 개수
return
X_pc : 투영된 데이터셋
'''
# M x N 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱 계산
sq_dists = pdist(X, 'sqeuclidean')
# 샘플 간의 거리를 정방 대칭 행렬로 변환
mat_sq_dists = squareform(sq_dists)
# 커널 행렬 계산
K = exp(-gamma * mat_sq_dists)
# 커널 행렬을 중앙에 맞춤
'''
표준화된 데이터에서 비선형 특성 조합으로 점곱을 대체할 때 사용한
모든 특성의 평균은 0이다. 하지만 새로운 특성 공간을 명시적으로 계산하지
않기 때문에 중앙에 맞춰져 있다는 보장이 없기 때문에 중앙에 맞춘다.
'''
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 중앙에 맞춰진 커널 행렬의 고유값과 고유벡터를 구함
# scipy.linalg.eigh 함수는 오름차순 반환
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
# 최상위 k개의 고유 벡터를 선택 (투영결과)
X_pc = np.column_stack([eigvecs[:, i] for i in range(n_components)])
return X_pc
3) Sklearn kernel PCA
from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples = 100, random_state = 123)
scikit_kpca = KernelPCA(n_components = 2, kernel = 'rbf', gamma = 15)
X_skernpca = scikit_kpca.fit_transform(X)Kernal SVM
Support Vector Machine; SVM
Support Vector Machine - 고차원 데이터 분류에 좋은 성능을 보인다. - 퍼셉트론의 확장 - 최적화 대상은 margin을 최대화하는 것 margin : 클래스를 구분하는 결정 경계와 결정 경계와 가장 가까운 sample사
sjpyo.tistory.com
참고
www.eric-kim.net/eric-kim-net/posts/1/kernel_trick_blog_ekim_12_20_2017.pdf
머신러닝 교과서 (길벗)
'Data > Data preprocessing' 카테고리의 다른 글
| Sampling unbalanced data (1) | 2021.02.23 |
|---|---|
| Feature Extraction (PCA, LDA) (0) | 2021.02.21 |
| Data Scaling (normalization, standardization) (0) | 2021.02.19 |
| Categorical variables encoding / mean, one-hot, label (0) | 2021.01.22 |
| Feature selection (변수 선택) (0) | 2021.01.17 |
