Sampling (표본추출)
1) 개요
- 모집단에서 표본을 추출해내는 것
- 모집단 또는 표본을 요약하기 위해 평균, 분산을 계산한다.
| Mean | Variance | |
| Population | $$\mu$$ | $$\sigma^{2}$$ |
| Sample | $$\overline{X}$$ | $$S^{2}$$ |
2) Statistic (통계량)
- 샘플들의 함수로 정의된다.
- 샘플평균, 샘플분산도 통계량 중 하나이다.
$$Statistic = f(x_{1}, x_{2}, \cdots, x_{n})$$
$$\overline{X} = \frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$$
$$S^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{X})^{2}$$
3) Sampling distribution of Sample Mean
- 통계량의 분포
- 확률변수 n개가 independent, identically, distributed하며 정규분포를 따른다.
- X bar의 기대값
$$E[\overline{X}] = E[\frac{1}{n}(X_{1}+X_{2}+ \cdots + X_{n})]$$
$$= \frac{1}{n}E[X_{1}] + \cdots + \frac{1}{n}E[X_{n}]$$
$$= \frac{1}{n}\mu + \cdots + \frac{1}{n}\mu$$
$$= n\cdot \frac{1}{n}\cdot \mu = \mu$$
- X bar의 분산
$$V[\overline{X}] = V[\frac{1}{n}(X_{1}+X_{2}+ \cdots + X_{n})]$$
$$= \frac{1}{n^{2}}V[X_{1}] + \cdots + \frac{1}{n^{2}}V[X_{n}]$$
$$= \frac{1}{n^{2}}\sigma^{2} + \cdots + \frac{1}{n^{2}}\sigma^{2}$$
$$= n\cdot \frac{1}{n^{2}}\cdot \sigma^{2} = \frac{\sigma^{2}}{n}$$
- X bar의 표준정규분포
$$Z = \frac{\overline{X} - \mu}{\sigma / \sqrt{n}} \Rightarrow N(0, 1)$$
4) 두 모집단 간의 기대값, 분산의 차이
- 기대값
$$E[\overline{X}_{1}-\overline{X}_{2}] = E[\overline{X}_{1}] - E[\overline{X}_{2}] = \mu_{1} - \mu_{2}$$
- 분산
$$V(\overline{X}_{1}-\overline{X}_{2}) = V(\overline{X}_{1}) + V(\overline{X}_{2}) = \frac{\sigma_{1}^{2}}{n_{1}} + \frac{\sigma_{2}^{2}}{n_{2}}$$
5) Sampling distribution of Sample Variance
- 모집단의 분포가 정규분포를 따르면 샘플은 independent, identically, distributed 하다.
- 표본 분산은 카이제곱 분포 n-1의 자유도를 따른다.
- n : 샘플의 개수
$$\frac{(n-1)S^{2}}{\sigma^{2}}\;is\;distributed\;\chi^{2}(n-1)$$
자유도 : 예를 들어, 5개의 샘플이 있고 4개의 값만 알려져 있다. 이때, 5개 샘플 모두의 합이 정해져 있을 경우, 나머지 1개의 값은 자동으로 정해진다. 이때의 자유도는 4이다.
모집단은 모두 정규분포이다.
Chi-Square Distribution
1) 정의
- 표준정규분포(standard normal distribution)의 제곱의 합으로 만들어진 분포이다.
- v : 자유도 (freedom)= n-1 (n: 샘플의 개수)
$$Z = Z_{1}^{2}+Z_{2}^{2}+ \cdots + Z_{v}^{2}$$
$$Z \sim \chi^{2}(v)$$

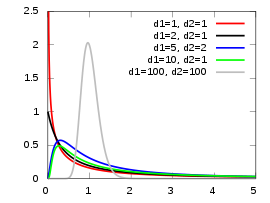
2) pdf
$$f_{x}(x; v) = \frac{1}{2^{v/2}\Gamma(\frac{v}{2})}x^{\frac{v}{2}-1}e^{\frac{-x}{2}}\;\;\;for\;\;x>0$$
3) 기대값과 분산
$$E[X] = v\;\;\;\;\;\;\; V(X)=2v$$
4) 감마분포와의 관계
- 감마분포의 alpha = v/2 이고 lambda = 2인 경우 카이제곱이다.
t Distribution
1) 정의
- Z가 N(0, 1)이고 Y가 카이제곱일 때, 다음과 같이 정의된다.
$$T = \frac{Z}{\sqrt{(Y/v)}}$$
$$T = \frac{\overline{X}-\mu}{S/\sqrt{n}}$$

2) 특징
- T는 t(v)로 나타나는 v의 자유도를 가지고 있는 T분포이다.
- T ~ t(n-1)
- E[T] = 0 (0을 기점으로 대칭성이 존재)
- 표준정규분포에 비해 꼬리가 길다.
- 모집단의 표준편차를 모를 경우, t 분포를 사용한다.
F Distribution
1) 정의
- Y1 (v1), Y2 (v2) 모두 카이제곱분포를 따를 때,
$$F = \frac{Y_{1}/v_{1}}{Y_{2}/v_{2}}$$
- Parameter : v1, v2 ~ F(v1, v2)
Central Limit Theorem (중심극한정리)
1) 정의
- 샘플 사이즈(n)가 클때, 모집단의 분포의 종류에 상관없이 표본평균(X bar)은 근사적으로 정규분포를 따른다. (일반적으로 n >= 30)
고려대 김성범 교수님의 유튜브를 정리하였습니다.
'Math > Probability & Statistics' 카테고리의 다른 글
| 분산, 공분산, 상관관계, 기대값의 특성 (0) | 2021.02.17 |
|---|---|
| Joint Probability Distribution (결합확률분포), Convolution (0) | 2021.02.17 |
| 연속형 확률 변수 (0) | 2021.02.16 |
| 이산형 확률분포 (0) | 2021.02.15 |
| 확률 변수 (Random Variable) (0) | 2021.02.15 |
